Part 1: univariate time series + classification

Intro

Time series processing is a well-known and extensively researched problem. Moreover - many people naturally understand, what a time series is, and how it is structured. Things start to get complicated once you are about to prepare time-dependent data for modeling with neural networks. Three-dimensional structures are not that easy to imagine initially. After reading this blog post, you will:

1. Understand the data should be pre-processed for LSTM neural networks;
2. Understand the benefits of keeping time-dependent structures in data;
3. See a practical example of wrongly and correctly prepared data for LSTM. Technologies used in this post are:
4. Pandas
5. Numpy
6. Tensorflow/Keras.

The code can be found: here.

Univariate ts

Univariate time-series data is nothing more than a vector of scalar (single values) observations recorded sequentially [NIST/SEMATECH e-Handbook of Statistical Methods]. In typical use-case scenarios (like stock price modeling or evaluating some processes happening in real life), the vector is indexed by time: days, minutes, seconds, etc… An example is presented below - a stock prices data, indexed by time and presented on a chart:

Libraries like Pandas have many functionalities related to time-series processing. Most of them are self-explanatory: you’re working with a flat vector of numbers. A detailed tutorial and explanations on this topic can be found in the official Pandas documentation.

Neural networks & ts data

Time-series data becomes problematic when we want to use it with neural networks. Of course, our goal is to keep the time-dependence, as we might believe, that it carries some important information.

A family of neural networks (NN) architecture that is naturally designed to consume that kind of data is called “Recurrent Neural Networks” (RNN), nowadays mainly represented by Long-Short Term Memory (LSTM) or Gated-Recurrent Unit (GRU) NNs*.

*We won’t discuss Transformers and Attention layers here, as they are players in their own league :)

In this post, we will discuss a classification task, so operation called: “many-to-one”. In this scenario, LSTM:

1. Takes a time-series data as an input;
2. Passes it step-by-step through the network;
3. Predicts a given class.

You can read more (and see some interesting visualizations) on the Stanford University CS230 Recurrent Neural Networks Course website [Stanford CS 230 - Recurrent Neural Networks ].

Notation

Before we proceed, let’s introduce some notation. It will be much easier to operate on symbols instead of describing everything in words :)

$$ \begin{align*} N -& \text{ number of time windows (samples) to consider} & \\\ y_i^t -& \text{ observation in the moment t, that belongs to ith sample} & \\\ T -& \text{ maximal time-window size} & \\\ h -& \text{ LSTM units} & \\\ c -& \text{ number of classes} & \\\ f -& \text{ number of features (unique time series) to use} \end{align*} $$

In this tutorial, we will operate on univariate time series, so f=1 every time

Data structures

LSTMs require a particular data format that preserves a time-dependence and keeps data at least three-dimensional. What a typical LSTM network need is the following shape:

$$ N \times T \times F $$

So a three-dimensional structure: no. of samples x time steps x features (=1 in this tutorial).

You might wonder - “what are these samples? How do we get samples from a time series? How do I know how many steps I should have?”. Let’s first discuss this problem theoretically and then - use some concrete, practical examples.

Choosing shape

How do we decide on the number of time steps T in our structure? Most of the time, it should be an “informed guess”. Number T will determine how large a piece of a time series the LSTM will receive in one go. In other words - how far-seeing will it be. The decision should be based on either:

1. The properties of the time series - seasonality, autocorrelation, trends, etc. How large is the period needed to capture some relevant info? You can obtain such information by classic time-series decomposition using statistical analysis.
2. The business rationale behind the process - e.g., preexisting knowledge about the most informative length of the sequence (the typical length of the business process or seasonality of an event).
3. Previous studies or research presenting the optimal window size for a similar problem (e.g., time exposure to some stimulus).

However, you must be aware that classic recurrent neural networks, LSTMs, and GRUs are prone to vanishing or exploding gradients if the sequences are large. If the time window is too large, LSTM might start to “forget” what it has seen so far, leading (of course) to worsening the prediction results. This vulnerability is one of the reasons why special training techniques (like Truncated Backpropagation Through Time (TBTT) or Gradient Clipping) and architectures (attention layers and eventually Transformers) were designed. Although theoretically, LSTMs can handle sequences spanning a couple of hundred elements, it is better to shorten them and present in the form of limited-time windows [Mikolov, et al. 2013; Karpathy, 2015].

Slicing

Once we have decided the length of our time window, it is time to slice a time series. The operation is easy and relatively intuitive: we slide a window of size T, one element at a time, and save subsequent windows as samples. This is the way we obtain N samples.

It is easy to calculate the number of time-slices: it will be (K-T+1).

Let’s check if that’s true.

Imagine that we have:

• A time series of consecutive numbers from 0 to 90.
• They are indexed by dates from 01.01.2020 to 31.03.2020.
• We want to have a sliding time window of size 6.

Therefore in our calculation we will have: $$ K = 91 $$ $$ T = 6 $$ $$ N = (K-T+1) = 86 $$

The code snipped below presents:

1. How to construct such a time series.
2. How to slice it using pandas.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

def generate_lagged_data(y: pd.Series, k_lags: int) -> pd.DataFrame:
    """
    Generates a lagged time series data in a fromat y, y-1, y-2, ..., y-K up to
    K-th lag.

    Parameters
    ----------
    y : pd.Series
        Original time series.
    k_lags: int
        Number of lags to generate.

    Returns
    ----------
    pd.DataFrame
        A lagged dataframe in format y, y-1, y-2, ..., y-K.
    """
    data = pd.DataFrame({'y': y})
    for t in range(k_lags):
        fname = f"y-{t}" if t > 0 else "y"
        lagged = y.shift(t)
        data[fname] = lagged
    return data

example_ts = pd.Series(np.arange(10))
generate_lagged_data(example_ts, 4).dropna()

Output from this function looks like this:

LSTM prep

There is one more thing missing. As described above, LSTM expects the data in the following format: $$ N \times K \times f $$

where f is a number of features. In our case, f = 1 because we want to analyze only one time series. So, we can use numpy’s expand_dims function to add this one missing dimension:

1
2

lagged_example_for_lstm = lagged_example.values.reshape((lagged_example.shape[0], 5, 1))
lagged_example_for_lstm.shape

As we can see, now the shape is ready to be utilized with an LSTM network.

Practical example

The problem

Let’s imagine the following situation: we have three different processes, logging some information over time. These might be some sensors, loggers, or robots; details do not matter. Each of these traces has a different characteristic and morphology of a signal.

The data

I want to keep this tutorial simple, without unnecessary details and additional functions. Therefore, let’s create some artificial data with different characteristics and assign labels 0, 1, and 2.

1
2
3
4

x = np.linspace(start=0, stop=500, num=1000)
y1 = np.sin(x) + np.random.normal(size=x.shape[0], loc=0, scale=0.5)
y2 = np.sin(0.05*x) + np.sin(0.3* np.pi * x) + np.random.normal(size=x.shape[0], loc=0, scale=0.5)
y3 = np.sin(2 * x) +  np.sin(0.5 * 2 * x) + np.random.normal(size=x.shape[0], loc=0, scale=0.5)

To make things a bit harder for the algorithm, I have added some slight random noise to functions (line 2,3,4) so that it won’t be 100% aligned with the perfect sinusoid equation.

Once we have done that, we can utilize our function for building lagged time series to prepare time slices for each process. We will use K = 10 lags here (9 lags + so-called lag-0: the “current” time).

1
2
3
4
5
6
7
8

NLAGS = 9
lagged_y1 = generate_lagged_data(pd.Series(y1), NLAGS).dropna()
lagged_y1['cls'] = 0
lagged_y2 = generate_lagged_data(pd.Series(y2), NLAGS).dropna()
lagged_y2['cls'] = 1
lagged_y3 = generate_lagged_data(pd.Series(y3), NLAGS).dropna()
lagged_y3['cls'] = 2
all_data = pd.concat([lagged_y1, lagged_y2, lagged_y3], ignore_index=True)

The data is presented on chart below. Double-click a legend to isolate a single time series. You can also zoom in and slice it.

The experiment

We will keep the last 20% of the data samples as a test set, and the remaining will be mixed up together and used during training.

We will normalize the training data and use normalizer trained on it to do the same with test data. Similar things can be achieved by building a pipeline (combining an LSTM with Scaler), but let’s keep things simple here.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

def build_train_test_data(series: List[pd.DataFrame], test_perc: float = 0.2) -> Tuple[pd.DataFrame, pd.DataFrame]:
    """
    Builds a train-test dataset using a time-split method. 
    We will keep last test_prec of each time series as a test set, training on the remaining data.
    """
    train_data = pd.DataFrame()
    test_data = pd.DataFrame()
    for ts in series:
        test_nobs = int(test_perc * ts.shape[0])
        ts_train = ts.iloc[:-test_nobs]
        ts_test = ts.tail(test_nobs)
        
        train_data = pd.concat([train_data, ts_train], ignore_index=True)
        test_data = pd.concat([test_data, ts_test], ignore_index=True)
    return train_data, test_data

train, test = build_train_test_data([lagged_y1, lagged_y2, lagged_y3])
scaler = StandardScaler()

X_train, X_test = train.drop(columns='cls'), test.drop(columns='cls')
y_train, y_test = train.cls, test.cls
X_train = np.expand_dims(scaler.fit_transform(X_train), -1)
X_test = np.expand_dims(scaler.transform(X_test), -1)

y_train_ohe = krs.utils.to_categorical(y_train, num_classes=3)
y_test_ohe = krs.utils.to_categorical(y_test, num_classes=3)

We can take a look on a single sample in X_train. This is just a part of some sinusoid, a slice of the curve.

Now it’s time to conduct our experiment. As a baseline to compare with, we will use random guessing with prior probability :) We would expect our model to be better than that. The architecture for this LSTM has been arbitrarily chosen - it’s not the main point of this exercise, so repeated cross-validation or using Keras Tuner for finding the best hyperparameters is beyond the scope of this post.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

def build_model() -> krs.Model:
    """
    Builds a Keras model. A wrapper function for SciKeras.
    """
    inp = krs.layers.Input(shape=(NLAGS+1, 1))
    lstm_out = krs.layers.LSTM(32)(inp)
    dense1 = krs.layers.Dense(16, activation='relu')(lstm_out)
    dense2 = krs.layers.Dense(16, activation='relu')(dense1)
    out = krs.layers.Dense(3, activation='softmax')(dense2)
    model = krs.models.Model(inputs=inp, outputs=out)
    model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy', krs.metrics.Precision(), krs.metrics.Recall()])
    return model

model_wrapper = KerasClassifier(build_model, epochs=10, batch_size=32, verbose=0)
dummy = DummyClassifier(strategy='stratified', random_state=123)
f1 = make_scorer(lambda y_true, y_pred: f1_score(y_true, y_pred, average='micro'))
kf = KFold(n_splits=10)
model_cv = cross_val_score(model_wrapper, X_train, y_train_ohe, cv=kf, scoring=f1, n_jobs=10)
dummy_cv = cross_val_score(dummy, X_train, y_train_ohe, cv=kf, scoring=f1, n_jobs=10)
cv_scores = pd.DataFrame({'LSTM': model_cv, 'Dummy': dummy_cv})

In the experiment, the following things happened:

• Lines 1-12: Wrap model building into function so it can be later used by Scikit-learn API.
• Line 14: Use Scikeras API to make Keras model usable within cross-validation
• Line 15: Prepare a dummy classifier that randomly predicts classes based on their prior probability.
• Line 16: Prepare a model metric for comparison: micro-averaged F1 score.
• Line 17-19: Perform repeated stratified K-fold cross-validation on each model using the metric provided.
• Line 20: Save all metrics in a one data frame for later comparison

The model is trained, so let’s evaluate it on the test set. And use a non-parametric statistical test to compare the statistical significance of the results against a random baseline.

To compare results, we will utilize the non-parametric Wilcoxon signed-rank test. Non-parametric tests are recommended every time; we cannot guarantee that strict assumptions, e.g., normality of errors, heteroskedasticity, independence of samples, etc., are not violated [Salzberg 1997 ;Demšar, 2006]. Our null hypothesis is that there is no difference between the two classifiers. An alternative hypothesis is that the difference is present in favor of an LSTM. We will conduct a test on a significance level alpha = 0.05 (meaning that we accept only a 5% chance that observed results are accidental).

Checking the model on test data:

1
2
3
4

model = build_model()
history = model.fit(X_train, y_train_ohe, epochs=10, batch_size=32)
yhat_lstm = model.predict(X_test).argmax(axis=1)
classification_report(y_test, yhat_lstm)

          precision    recall  f1-score   support

       0       0.85      0.86      0.85       198
       1       0.91      0.83      0.87       198
       2       0.89      0.95      0.92       198

accuracy                           0.88       594
macro avg      0.88      0.88      0.88       594
weighted avg   0.88      0.88      0.88       594

Statistical comparison of cross val scores:

1
2

fig = sns.boxplot(data=cv_scores);
fig.set_title("Results comparison");

1

st.wilcoxon(model_cv, dummy_cv, alternative='greater')

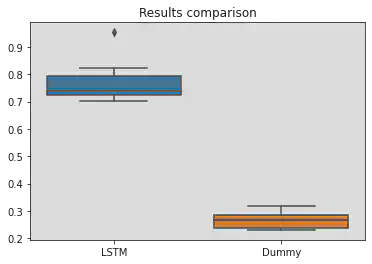
WilcoxonResult(statistic=55.0, pvalue=0.0009765625)

As we can see by a naked eye: the LSTM model outperformed random choice significantly. Our statistical test allows us to reject the null hypothesis :)

Wrong approach

You might wonder - “ok, but what will happen if I ignore the time dependence and just sample points at random from each process. This is an easy task - each curve is a sinusoid with a characteristic morphology - if we sample enough data points, it should be sufficient to recognize a typical range of values for each type”. Here we treat each data point as an iid datum - independent from others but from the same characteristic distribution, specific for each class. So we will turn the whole exercise into a typical classification problem from tabular data.

We might ignore for a while the fact that this is the fundamentally wrong approach because the problem IS a time series classification and check if it’s going to work after all. Let’s try: we skip the lagging part entirely and randomly sample data points for each class. To make it easier for the algorithm: we will sample with a replacement for each time series so that the algorithm may see the same data points twice: in training and testing. It should be easy, shouldn’t it? We will use one of the Gradient Boosting family models to model such data.

Data samples without time dependence preparation:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

def generate_iid_data(ts: np.array, label: int, n_features: int, nsamp: int) -> pd.DataFrame:
    """
    Generates random samples with replacement, assuming that the data is IID. It does not preserve
    a time dependence and samples each data point multiple times.
    """
    rnd_features = {}
    for idx in range(n_features):
        rnd_feature = np.random.choice(ts, size=nsamp, replace=True)
        rnd_features[f"f_{idx}"] = rnd_feature
    rnd_df = pd.DataFrame(rnd_features)
    rnd_df['y'] = label
    return rnd_df

rnd_data = pd.DataFrame()
for idx, ts in enumerate([y1, y2, y3]):
    df = generate_iid_data(ts, idx, NLAGS+1, 800)
    rnd_data = pd.concat([rnd_data, df], ignore_index=True)
rnd_data.shape

The experiment:

1
2
3
4
5

X_rnd, y_rnd = rnd_data.drop(columns='y'), rnd_data.y
X_train_rnd, X_test_rnd, y_train_rnd, y_test_rnd = train_test_split(X_rnd, y_rnd, train_size=0.8, random_state=123)

xgb_clf = xgb.XGBClassifier(max_depth=10, learning_rate=0.01, n_estimators=500)
xgb_rnd_cv = cross_val_score(xgb_clf, X_train_rnd, y_train_rnd, cv=kf, scoring=f1)

Collecting the cv scores and comparison:

1
2

cv_scores['xgboost'] = xgb_rnd_cv
sns.boxplot(data=cv_scores)

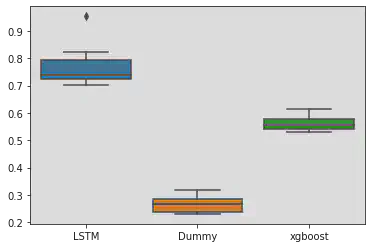
XGboost prediction on test data:

1
2
3
4

xgb_clf = xgb.XGBClassifier(max_depth=10, learning_rate=0.01, n_estimators=500)
xgb_clf.fit(X_train_rnd, y_train_rnd)
yhat_xgb = xgb_clf.predict(X_test_rnd)
print(classification_report(y_test_rnd, yhat_xgb))

            precision    recall  f1-score   support

          0       0.61      0.81      0.70       149
          1       0.54      0.51      0.52       158
          2       0.54      0.42      0.47       173

  accuracy                           0.57       480
  macro avg      0.57     0.58       0.57       480
  weighted avg   0.56     0.57       0.56       480

As we can see, such a classifier performs much worse than our previous model. Clearly, it possesses SOME skill - points that belong to common distribution shuffled at random definitely share some properties, but it is not enough to achieve satisfactory results.

For the sake of completeness and reliability, let’s perform a non-parametric equivalent of ANOVA: a Friedman chi-square test, suitable for comparing multiple algorithms on multiple datasets [Demšar, 2006]. Our null hypothesis is that there is no significant difference between models. An alternative hypothesis: is that such a difference exists. Suppose we manage to reject the null hypothesis. In that case, we will perform a pairwise, post-hoc non-parametric test to detect differences between pairs of classifiers with corrected p-value to control the false discovery rate [Trawinski et al. 2012].

Overall Friedmann test:

1

pg.friedman(data=cv_scores)

Pairwise comparison

1

pg.pairwise_ttests(cv_scores.melt(), between='variable', dv='value', parametric=False).round(5)

And again, there are no surprises here. We can safely reject the null hypothesis and (after pairwise testing) see clearly, that LSTM, preserving time-dependence, performs much better than XGBoots, even after aggressive resampling with replacement.

Summary

The points below briefly summarize what has been discussed in this blogpost:

1. LSTM requires data in a format: N samples x T time steps x F features.
2. For univariate time series, F = 1, so the data shape becomes N x T x 1 Such a structure can be generated from data by subsequent shifting the time series.
3. A predictive model that preserves the time-dependence performs much better than random sampling, which treats the data as iid. This is a fundamentally wrong approach for such problems.

Bibliography

1. CS 230 - Recurrent Neural Networks Cheatsheet; https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks

2. Demšar, J. (2006) “Statistical comparisons of classifiers over multiple data sets”, Journal of Machine learning research, nr 7(Jan), ss. 1–30

3. Exploding & vanishing problem: Pascanu, R., Mikolov, T., & Bengio, Y. (2013, May). On the difficulty of training recurrent neural networks. In International conference on machine learning (pp. 1310-1318). PMLR. https://arxiv.org/pdf/1211.5063.pdf

4. NIST/SEMATECH e-Handbook of Statistical Methods, https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc41.htm, 29.04.2022

5. Reasonable choices: Blog, Karpathy A. (2015). The Unreasonable Effectiveness of Recurrent Neural Networks. URL: http://karpathy. github.io/2015/05/21/rnn-effectiveness/dated May 21, 33.

6. Salzberg, S. L. (1997) “On comparing classifiers: Pitfalls to avoid and a recommended approach”, Data mining and knowledge discovery. Springer, nr 1(3), ss. 317–328

7. Trawinski, B. et al. (2012) “Nonparametric statistical analysis for multiple comparison of machine learning regression algorithms”, International Journal of Applied Mathematics and Computer Science, nr 22(4), ss. 867–881. doi: 10.2478/v10006-012-0064-z